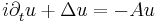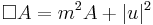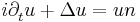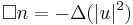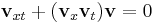List of nonlinear partial differential equations
In mathematics and physics, nonlinear partial differential equations are (as their name suggests) partial differential equations with nonlinear terms. They describe many different physical systems, ranging from gravitation to fluid dynamics, and have been used in mathematics to solve problems such as the Poincaré conjecture and the Calabi conjecture. They are difficult to study: there are almost no general techniques that work for all such equations, and usually each individual equation has to be studied as a separate problem.
Contents |
Methods for studying nonlinear partial differential equations
Existence and uniqueness of solutions
A fundamental question for any PDE is the existence and uniqueness of a solution for given boundary conditions. For nonlinear equations these questions are in general very hard: for example, the hardest part of Yau's solution of the Calabi conjecture was the proof of existence for a Monge-Ampere equation.
Singularities
The basic questions about singularities (their formation, propagation, and removal, and regularity of solutions) are the same as for linear PDE, but as usual much harder to study. In the linear case one can just use spaces of distributions, but nonlinear PDEs are not usually defined on arbitrary distributions, so one replaces spaces of distributions by refinements such as Sobolev spaces.
An example of singularity formation is given by the Ricci flow: Hamilton showed that while short time solutions exist, singularities will usually form after a finite time. Perelman's solution of the Poincaré conjecture depended on a deep study of these singularities, where he showed how to continue the solution past the singularities.
Linear approximation
The solutions in a neighborhood of a known solution can sometimes be studied by linearizing the PDE around the solution. This corresponds to studying the tangent space of a point of the moduli space of all solutions.
Moduli space of solutions
Ideally one would like to describe the (moduli) space of all solutions explicitly, and for some very special PDEs this is possible. (In general this is a hopeless problem: it is unlikely that there is any useful description of all solutions of the Navier–Stokes equation for example, as this would involve describing all possible fluid motions.) If the equation has a very large symmetry group, then one is usually only interested in the moduli space of solutions modulo the symmetry group, and this is sometimes a finite dimensional compact manifold, possibly with singularities; for example, this happens in the case of the Seiberg-Witten equations. A slightly more complicated case is the self dual Yang-Mills equations, when the moduli space is finite dimensional but not necessarily compact, though it can often be compactified explicitly. Another case when one can sometimes hope to describe all solutions is the case of completely integrable models, when solutions are sometimes a sort of superposition of solitons; for example, this happens for the Korteweg–de Vries equation.
Exact solutions
It is often possible to write down some special solutions explicitly in terms of elementary functions (though it is rarely possible to describe all solutions like this). One way of finding such explicit solutions is to reduce the equations to equations of lower dimension, preferably ordinary differential equations, which can often be solved exactly. This can sometimes be done using separation of variables, or by looking for highly symmetric solutions.
Some equations have several different exact solutions.
Numerical solutions
Numerical solution on a computer is almost the only method that can be used for getting information about arbitrary systems of PDEs. There has been a lot of work done on solving certain systems numerically, especially for the Navier–Stokes and other equations related to weather prediction.
Lax pair
If a system of PDEs can be put into Lax pair form
then it usually has an infinite number of first integrals, which help to study it.
Euler-Lagrange equations
Systems of PDEs often arise as the Euler-Lagrange equations for a variational problem. Systems of this form can sometimes be solved by finding an extremum of the original variational problem.
Hamilton equations
Integrable systems
PDEs that arise from integrable systems are often the easiest to study, and can sometimes be completely solved. A well known example is the Korteweg–de Vries equation.
Symmetry
Some systems of PDEs have large symmetry groups. For example, the Yang-Mills equations are invariant under an infinite dimensional gauge group, and many systems of equations (such as the Einstein field equations) are invariant under diffeomorphisms of the underlying manifold. Any such symmetry groups can usually be used to help study the equations; in particular if one solution is known one can trivially generate more by acting with the symmetry group.
Sometimes equations are parabolic or hyperbolic "modulo the action of some group": for example, the Ricci flow equation is not quite parabolic, but is "parabolic modulo the action of the diffeomorphism group", which implies that it has most of the good properties of parabolic equations.
Look it up
There are several tables of previously studied PDEs such as (Polyanin & Zaitsev 2004) and (Zwillinger 1998) and the tables below.
List of equations
A–F
| Name | Dim | Equation | Applications |
|---|---|---|---|
| Benjamin–Bona–Mahony | 1+1 | 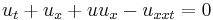 |
Fluid mechanics |
| Benjamin-Ono | 1+1 | 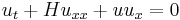 |
internal waves in deep water |
| Boomeron | 1+1 | 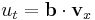
|
Solitons |
| Born-Infeld | 1+1 | 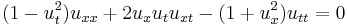 |
|
| Boussinesq | 1+1 | 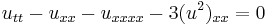 |
Fluid mechanics |
| Buckmaster | 1+1 | 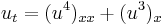 |
Thin viscous fluid sheet flow |
| Burgers | 1+1 | 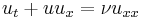 |
Fluid mechanics |
| Cahn-Hilliard equation | Any | 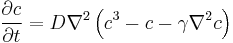 |
Phase separation |
| Calabi flow | Any | Calabi-Yau manifolds | |
| Camassa–Holm | 1+1 | 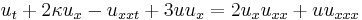 |
Peakons |
| Carleman | 1+1 | 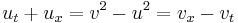 |
|
| Cauchy momentum | any | 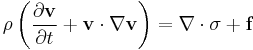 |
Momentum transport |
| Caudrey-Dodd-Gibbon- Sawada-Kotera | 1+1 | Same as (rescaled) Sawada-Kotera | |
| Chiral field | 1+1 | ||
| Clairaut equation | any | 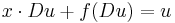 |
Differential geometry |
| Complex Monge-Ampère | Any | 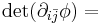 lower order terms lower order terms |
Calabi conjecture |
| Davey–Stewartson | 1+2 | 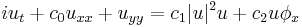
|
Finite depth waves |
| Degasperis-Procesi | 1+1 | 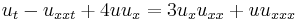 |
Peakons |
| Dispersive long wave | 1+1 | 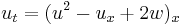 , , 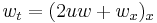 |
|
| Drinfel'd -Sokolov -Wilson | 1+1 | 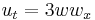
|
|
| Dym equation | 1+1 | 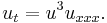 |
Solitons |
| Eckhaus equation | 1+1 | 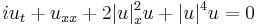 |
Integrable systems |
| Eikonal equation | any | 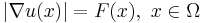 |
optics |
| Einstein field equations | Any | 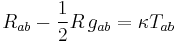 |
General relativity |
| Ernst equation | 2 | 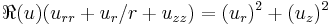 |
|
| Euler equations | 1+3 | ![\begin{align}
&{\partial\rho\over\partial t}%2B
\nabla\cdot(\rho\bold u)=0\\[1.2ex]
&{\partial\rho{\bold u}\over\partial t}%2B
\nabla\cdot(\bold u\otimes(\rho \bold \bold u))%2B\nabla p=0\\[1.2ex]
&{\partial E\over\partial t}%2B
\nabla\cdot(\bold u(E%2Bp))=0,
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/b5cad567928ffa0c047a846b2b8b76ee.png) |
non-viscous fluids |
| Fisher's equation | 1+1 | 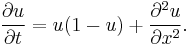 |
Gene propagation |
| Fitzhugh-Nagumo | 1+1 | 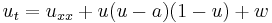
|
G–K
| Name | Dim | Equation | Applications |
|---|---|---|---|
| Gardner equation | 1+1 | 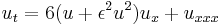 |
|
| Garnier equation | isomonodromic deformations | ||
| Gauss-Codazzi | surfaces | ||
| Ginzburg-Landau | 1+3 | 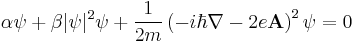 |
Superconductivity |
| Gross-Neveu | 1+1 | ||
| Gross –Pitaevskii | 1+n | 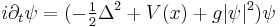 |
Bose–Einstein condensate |
| Hartree equation | Any | 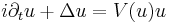
where |
|
| Hasegawa-Mima | 1+3 | 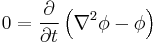
|
Turbulence in plasma |
| Heisenberg ferromagnet | 1+1 | 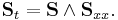 |
Magnetism |
| Hirota equation | 1+1 | ||
| Hirota -Satsuma | 1+1 | 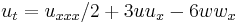 , ,
|
|
| Hunter–Saxton | 1+1 | 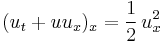 |
Liquid crystals |
| Ishimori equation | 1+2 | 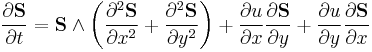
|
Integrable systems |
| Kadomtsev –Petviashvili | 1+2 | 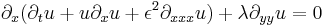 |
Shallow water waves |
| von Karman | 2 | 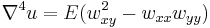 , , 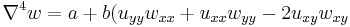 |
|
| Kaup | 1+1 | 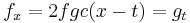 |
|
| Kaup –Kupershmidt | 1+1 | 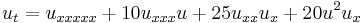 |
Integrable systems |
| Klein -Gordon -Maxwell | any | 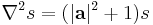 , , 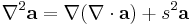 |
|
| Klein -Gordon (nonlinear) | any | 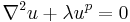 |
|
| Klein -Gordon -Zakharov | |||
| Khokhlov -Zabolotskaya | 1+2 | 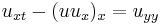 |
|
| Korteweg–de Vries (KdV) | 1+1 | 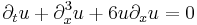 |
Shallow waves, Integrable systems |
| KdV (generalized) | 1+1 | 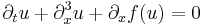 |
|
| KdV (modified) | 1+1 | 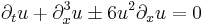 |
|
| KdV (super) | 1+1 | 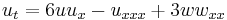 , , 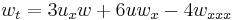 |
|
| There are more minor variations listed in the article on KdV equations. | |||
| Kuramoto -Sivashinsky | 1+n | 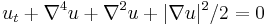 |
|
L–R
| Name | Dim | Equation | Applications |
|---|---|---|---|
| Landau–Lifshitz model | 1+n | 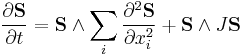 |
Magnetic field in solids |
| Lin-Tsien equation | 1+2 | 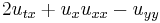 |
|
| Liouville | any | 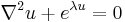 |
|
| Minimal surface | 3 | 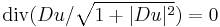 |
minimal surfaces |
| Molenbroeck | 2 | ||
| Monge–Ampère | any | 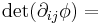 lower order terms lower order terms |
|
| Navier–Stokes (and its derivation) |
1+3 | ![\displaystyle
\rho \left( \frac{\partial v_i}{\partial t}
%2B v_j \frac{\partial v_i}{\partial x_j} \right) =
- \frac{\partial p}{\partial x_i}
%2B \frac{\partial}{\partial x_j} \left[
\mu \left( \frac{\partial v_i}{\partial x_j} %2B \frac{\partial v_j}{\partial x_i} \right)
%2B \lambda \frac{\partial v_k}{\partial x_k}
\right]
%2B f_i](/2012-wikipedia_en_all_nopic_01_2012/I/85c6f713ca94ac7b213cdb396ffa3d4e.png) + mass conservation: |
Fluid flow |
| Nonlinear Schrödinger (cubic) | 1+1 | 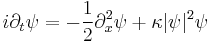 |
optics, water waves |
| Nonlinear Schrödinger (derivative) | 1+1 | 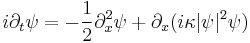 |
optics, water waves |
| Novikov–Veselov equation | 1+2 | see Veselov–Novikov equation below | |
| Omega equation | 1+3 | 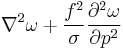 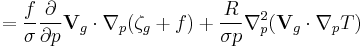 |
atmospheric physics |
| Plateau | 2 | 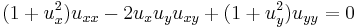 |
|
| Pohlmeyer -Lund -Regge | 2 | 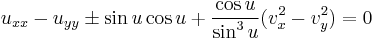
|
|
| Porous medium | 1+n | 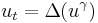 |
diffusion |
| Prandtl | 1+2 | 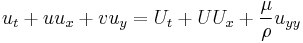 , , 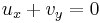 |
boundary layer |
| Primitive equations | 1+3 | Atmospheric models |
S–Z, α–ω
See also
- Euler-Lagrange equation
- Nonlinear system
- Integrable system
- Inverse scattering transform
- Dispersive partial differential equation
References
- Calogero, Francesco; Degasperis, Antonio (1982), Spectral transform and solitons. Vol. I. Tools to solve and investigate nonlinear evolution equations, Studies in Mathematics and its Applications, 13, Amsterdam-New York: North-Holland Publishing Co., ISBN 0-444-86368-0, MR0680040
- Pokhozhaev, S.I. (2001), "Non-linear partial differential equation", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=N/n067170
- Polyanin, Andrei D.; Zaitsev, Valentin F. (2004), Handbook of nonlinear partial differential equations, Boca Raton, FL: Chapman & Hall/CRC, pp. xx+814, ISBN 1-58488-355-3, MR2042347
- Scott, Alwyn, ed. (2004), Encyclopedia of Nonlinear Science, Routledge, ISBN 978-1579583859. For errata, see this
- Zwillinger, Daniel (1998), Handbook of differential equations (3rd ed.), Boston, MA: Academic Press, Inc., ISBN 978-0127843964, MR0977062
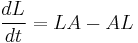
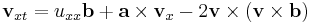
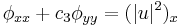
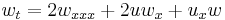
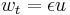
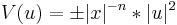 .
.![\displaystyle -\left[\left(\nabla\phi\times \mathbf{\hat z}\right)\cdot\nabla\right]\left[\nabla^2\phi-\ln\left(\frac{n_0}{\omega_{ci}}\right)\right]](/2012-wikipedia_en_all_nopic_01_2012/I/3166aaff680d341ba99f694a0a525d9b.png)
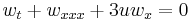
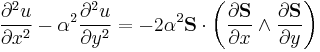
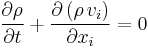
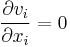
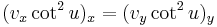
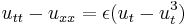
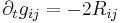
![\displaystyle \frac{\partial \theta}{\partial t}= \frac{\partial}{\partial z}
\left[ K(\psi) \left (\frac{\partial \psi}{\partial z} %2B 1 \right) \right]\](/2012-wikipedia_en_all_nopic_01_2012/I/070d4d5ee9a160b4d813a4fa5d0d0844.png)
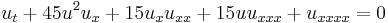
![\displaystyle
\begin{align}
{\partial A_i \over \partial t_j} &= {\left[ A_i, \ A_j \right] \over t_i - t_j}, \quad i\neq j \\
{\partial A_i \over \partial t_i} &=- \sum_{j=1 \atop j\neq i}^n {\left[ A_i, \ A_j \right] \over t_i - t_j}, \quad 1\leq i, j \leq n
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/d61710bb800a46e4a3a1dd616b001d27.png)

![\displaystyle
\begin{align}
\frac{\partial \eta }{\partial t} %2B \frac{\partial (\eta u)}{\partial x} %2B \frac{\partial (\eta v)}{\partial y} = 0\\[3pt]
\frac{\partial (\eta u)}{\partial t}%2B \frac{\partial}{\partial x}\left( \eta u^2 %2B \frac{1}{2}g \eta^2 \right) %2B \frac{\partial (\eta u v)}{\partial y} = 0\\[3pt]
\frac{\partial (\eta v)}{\partial t} %2B \frac{\partial (\eta uv)}{\partial x} %2B \frac{\partial}{\partial y}\left(\eta v^2 %2B \frac{1}{2}g \eta ^2\right) = 0
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/46758911cfafdb466dd2b58e7c773ba0.png)
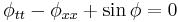
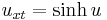
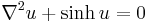
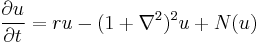
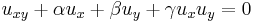
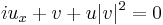 ,
, 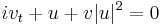
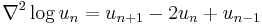
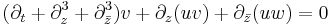 ,
, 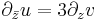 ,
, 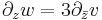
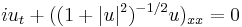
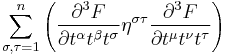
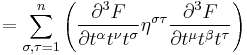
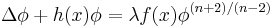
![\displaystyle D_\mu F^{\mu\nu}=0, \quad F_{\mu \nu} = A_{\mu, \nu} - A_{\nu, \mu }%2B [A_\mu, \, A_\nu]](/2012-wikipedia_en_all_nopic_01_2012/I/fa36602dc1ee50a2996548f936dfc1e8.png)
![F_{\alpha \beta} = \pm \epsilon_{\alpha \beta \mu \nu} F^{\mu \nu},
\quad F_{\mu \nu} = A_{\mu, \nu} - A_{\nu, \mu }%2B [A_\mu, \, A_\nu]](/2012-wikipedia_en_all_nopic_01_2012/I/7715bc42a25f8199b94decfa09d7f13e.png)